Bagging - Bootstrap Aggregation
Previously, we saw how ensemble methods, like averaging independent models or using bootstrap sampling, can reduce variance and improve prediction stability.
Today, we dive deeper into one powerful technique: Bagging — Bootstrap Aggregating, and explore how it helps build more stable and accurate models.
Bagging: Bootstrap Aggregation
Bagging, short for Bootstrap Aggregation, is a general-purpose method for reducing variance.
The idea is simple:
- Draw \(B\) bootstrap samples \(D_1, D_2, \dots, D_B\) from the original dataset \(D\).
-
Train a model on each bootstrap sample to get prediction functions:
\[\hat{f}_1, \hat{f}_2, \dots, \hat{f}_B\] -
Combine their predictions. The bagged prediction function is:
\[\hat{f}_{\text{avg}}(x) = \text{Combine}\left( \hat{f}_1(x), \hat{f}_2(x), \dots, \hat{f}_B(x) \right)\]
Depending on the task:
- For regression, we typically average predictions.
- For classification, we usually take a majority vote.
Key Point: Why Bagging Doesn’t Overfit
One of the most powerful aspects of bagging is that increasing the number of trees does not cause overfitting.
In fact, adding more trees generally improves performance by further reducing the variance of the model.
Since each tree is trained on a slightly different bootstrap sample, their errors tend to average out, making the overall prediction more stable and reliable.
Thus, more trees usually help — at worst, performance plateaus, but it rarely gets worse with additional trees.
Downside: Loss of Interpretability
However, this variance reduction comes at a cost. A single decision tree is often easy to visualize and interpret: you can follow a clear, logical path from the root to a prediction.
With hundreds or thousands of trees combined in a bagged ensemble, the resulting model becomes a black box — it is much harder (or nearly impossible) to trace a single prediction back through all contributing trees. In other words, bagging sacrifices interpretability for predictive performance.
Out-of-Bag (OOB) Predictions and Error Estimation
Bagging also provides a natural way to estimate test error without needing a separate validation set!
Recall:
- Each bagged model is trained on roughly 63% of the original data.
- The remaining 37% — the observations not included in the bootstrap sample — are called out-of-bag (OOB) observations.
For the \(i\)-th training point:
-
Define the set of bootstrap samples that did not include \(x_i\) as:
\[S_i = \{b \,\vert\, D_b \text{ does not contain } x_i\}\] -
The Out-of-Bag (OOB) prediction for \(x_i\) is then the average prediction across all trees where \(x_i\) was not used in training:
\[\hat{f}_{\text{OOB}}(x_i) = \frac{1}{|S_i|} \sum_{b \in S_i} \hat{f}_b(x_i)\]
Here, \(\vert S_i \vert\) is the number of trees that did not see \(x_i\) during training.
Once we have OOB predictions for all training points, we can compute the OOB error by comparing these predictions against the true labels.
The OOB error serves as a reliable estimate of the model’s test error — similar to cross-validation, but without needing to split the data or perform multiple rounds of training. This makes OOB evaluation very efficient, especially for large datasets.
Applying Bagging to Classification Trees
Let’s look at a practical example:
- Input space: \(X = \mathbb{R}^5\)
- Output space: \(Y = \{-1, 1\}\)
- Sample size: \(n = 30\)
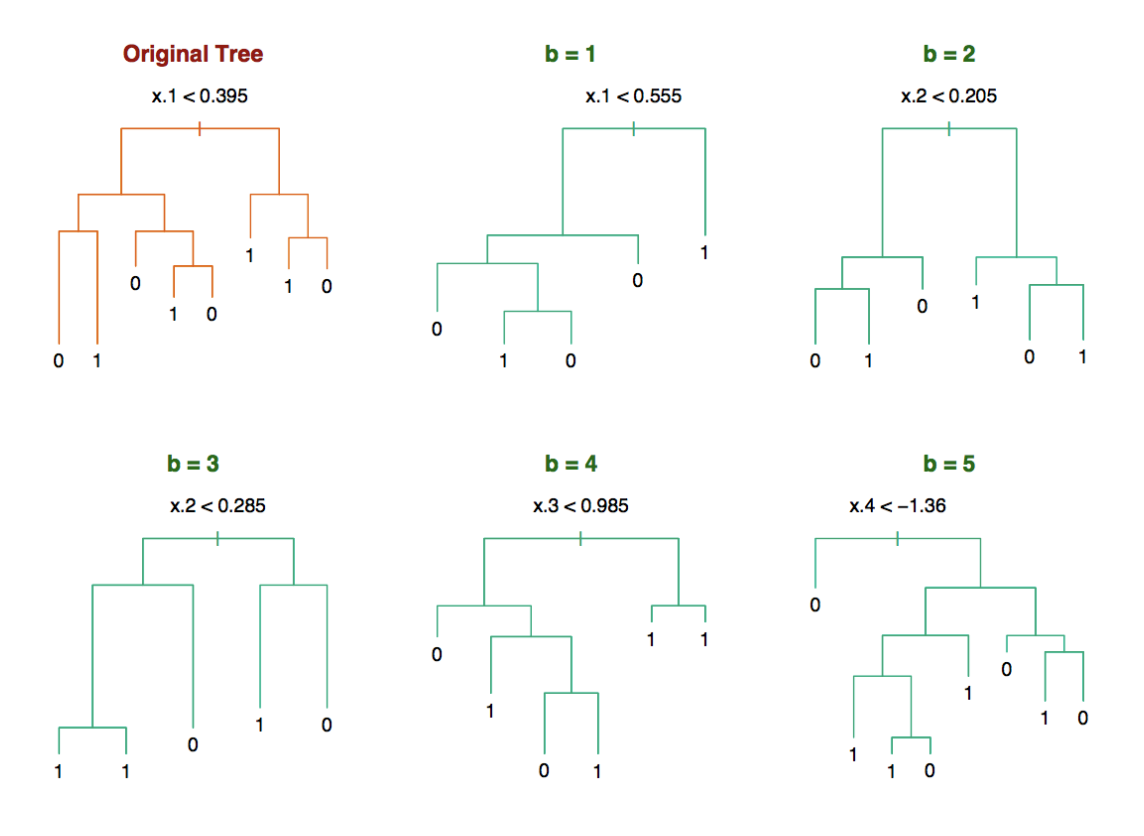
When we train decision trees on different bootstrap samples, the trees we get are often very different from one another.
- Each bootstrap sample is a slightly different version of the original dataset.
- As a result, the splitting variables chosen at the root (and deeper nodes) can change significantly across trees.
- This leads to trees with different structures, different decision boundaries, and ultimately, different predictions.
This behavior highlights a key property of decision trees: they are high variance models. Even small perturbations or changes in the training data can cause a decision tree to change substantially.
However, instead of seeing this as a disadvantage, we leverage this property through bagging (Bootstrap Aggregation). By training multiple high-variance trees on different bootstrap samples and averaging their predictions, we are able to:
- Reduce variance significantly
- Stabilize predictions
- Improve overall model performance without increasing bias
Thus, bagging turns the natural instability of decision trees into a strength, leading to a more robust and accurate ensemble model.
Why Decision Trees Are Ideal for Bagging
Bagging is particularly powerful when the base models are relatively unbiased but have high variance — and decision trees fit this description perfectly.
- Deep, unpruned decision trees tend to have low bias, as they can closely fit the training data and capture complex patterns.
- However, they also suffer from high variance: small changes or perturbations in the training data can lead to drastically different tree structures and predictions.
- By training many such high-variance trees on different bootstrap samples and averaging their outputs, bagging reduces the overall variance without significantly affecting the bias.
The result is a more stable, robust, and accurate ensemble model compared to relying on a single decision tree.
Thus, decision trees are an ideal candidate for bagging — their natural instability becomes an advantage when combined through this technique.
With this understanding in place, we are now ready to move toward an even more powerful idea: Random Forests - where we take bagging one step further by adding an extra layer of randomness to make our ensemble even stronger!