From Baseline to DeepSeek - Single-GPU MoE Training Efficiency
A systems-level analysis of training Mixture-of-Experts (MoE) Transformer models under single-GPU constraints. We compare naive PyTorch MoE, ScatterMoE, MegaBlocks, and DeepSeek-inspired architectures, revealing critical trade-offs between convergence behavior, memory footprint, and training throughput.
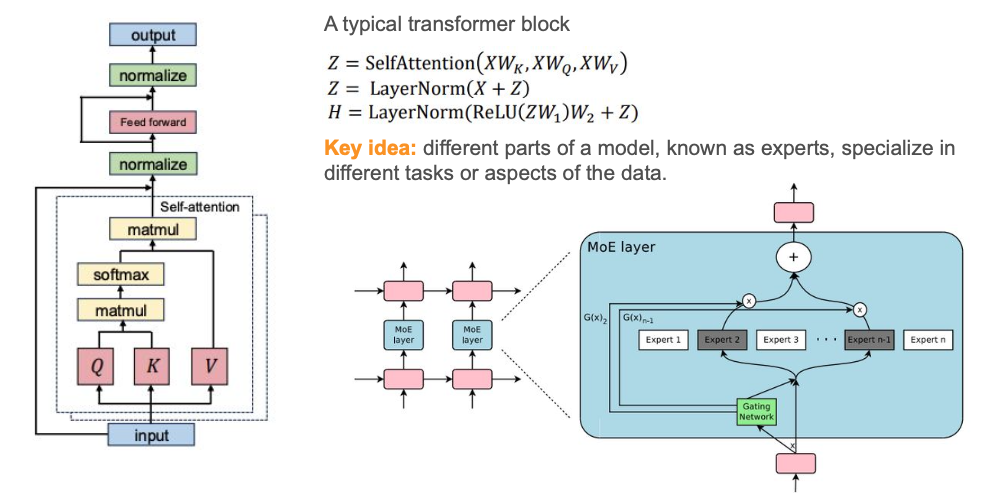
Recent advances in language modeling have been driven not only by architectural innovations, but also by improvements in training efficiency at the systems level. While Mixture-of-Experts (MoE) architectures have demonstrated strong efficiency gains in large-scale, multi-GPU deployments, their practical behavior on resource-constrained hardware remains poorly understood. We present a systems-oriented empirical study comparing dense Transformers with multiple MoE architectures on a single GPU, revealing that MoE designs optimized for distributed training do not directly translate to single-device settings.
This project was developed as part of the Big Data and Machine Learning course during the fall 2025 semester in the MSCS program at NYU Courant. Our team — Parvathi Biju and myself.
Introduction and Motivation
The modded-NanoGPT speedrun project exemplifies a systems-first perspective, focusing on identifying the fastest algorithms for training Transformer models under fixed hardware constraints. Inspired by this approach, we study Mixture-of-Experts (MoE) models through a systems lens, emphasizing practical performance and feasibility rather than theoretical scaling alone.
Transformers remain the dominant architecture for language modeling, but scaling dense models increases computation and memory costs proportionally. MoE architectures address this limitation by introducing conditional computation—routing each token to a small subset of expert networks and enabling parameter counts to scale independently of per-token compute. While MoEs have demonstrated strong efficiency gains in large-scale, multi-GPU deployments, their practical behavior on resource-constrained hardware remains poorly understood.
The Single-GPU Challenge
Training MoEs on a single GPU introduces unique challenges. Dynamic routing creates irregular computation patterns, expert load imbalance, and additional memory overhead from token dispatch and reordering. Existing MoE implementations are largely optimized for distributed environments, where large batch sizes and expert parallelism can amortize these costs. On consumer-grade GPUs, however, memory limits and kernel overhead become first-order constraints, making the choice of MoE implementation critical.
Research Questions
Our investigation focuses on three central questions:
- Memory Efficiency: How do different MoE implementations affect peak memory usage under single-GPU constraints?
- Training Throughput: What is the trade-off between kernel optimization and per-step latency?
- Convergence Quality: Do architectural choices (shared experts, routing strategies) impact final model performance independent of systems optimizations?
Key Contributions
- A single-GPU systems study of MoE training, grounded in the Modded NanoGPT framework and motivated by the speedrun philosophy of maximizing training efficiency under fixed hardware constraints
- An implementation-driven comparison of MoE designs, including naive PyTorch MoE, ScatterMoE, MegaBlocks, and a DeepSeek-inspired architecture
- An empirical analysis of throughput, memory footprint, and convergence behavior across MoE variants
- Practical insights into MoE feasibility on constrained hardware, clarifying when and why certain implementations become bottlenecked by memory or kernel overhead rather than compute
Background and Context
Mixture-of-Experts Architectures
Mixture-of-Experts (MoE) architectures introduce conditional computation into neural networks by routing each token to a small subset of expert networks. This design enables model capacity to scale independently of per-token compute and has been widely adopted in large language models.
The core MoE mechanism replaces a standard feed-forward layer with:
\[\text{MoE}(x) = \sum_{i=1}^{n} G(x)_i \cdot E_i(x)\]where $G(x)$ is a gating function (router) that produces routing weights, and $E_i(x)$ are expert networks. In top-k routing, only the k experts with highest routing scores are computed per token.
Expert Load Imbalancing
A central challenge in MoE training is expert load imbalance, which can lead to expert underutilization and degraded optimization. Prior work addresses this through auxiliary load-balancing losses that regularize routing behavior during training. While effective at scale, these mechanisms introduce additional optimization complexity and interact with systems-level constraints, particularly in non-distributed training regimes.
Modded NanoGPT Baseline
Modded NanoGPT represents a systems-optimized implementation of GPT-style Transformers, developed as part of the NanoGPT speedrun effort to identify the fastest training configurations under fixed hardware constraints. The framework combines:
- Compiled execution via
torch.compile - Memory-efficient Flash Attention
- Mixed-precision training (bfloat16)
- Optimized optimizer configurations (AdamW with fused kernels)
In this work, Modded NanoGPT serves as our strong dense baseline against which the systems overheads and benefits of different MoE implementations are evaluated.
MoE Implementation Variants
ScatterMoE
ScatterMoE proposes a routing-centric optimization for MoE layers by fusing token dispatch, expert computation, and output aggregation into a single kernel. This approach reduces routing overhead and intermediate memory traffic relative to naive MoE implementations.
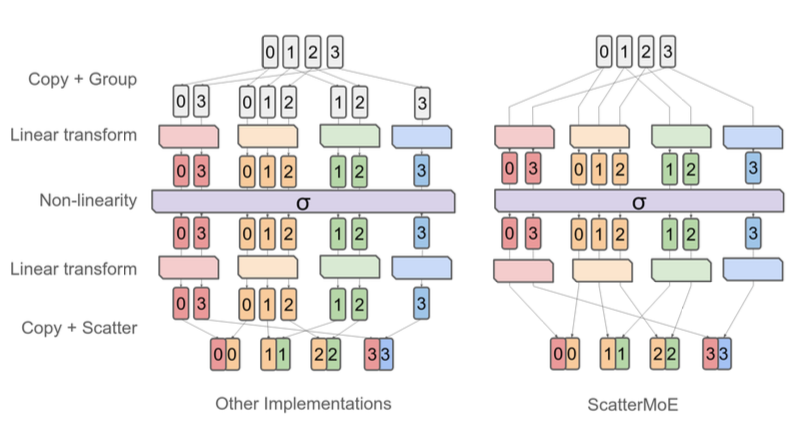
Key benefits:
- Lower memory footprint due to fused operations
- Reduced routing overhead from eliminated intermediate tensors
- Well-suited for moderate expert counts and batch sizes
MegaBlocks
MegaBlocks reformulates MoE computation as block-sparse matrix multiplication to efficiently handle load-imbalanced expert assignments. By expressing expert execution as grouped matrix operations over dynamically constructed sparse blocks, MegaBlocks achieves high arithmetic efficiency in large-scale training regimes.
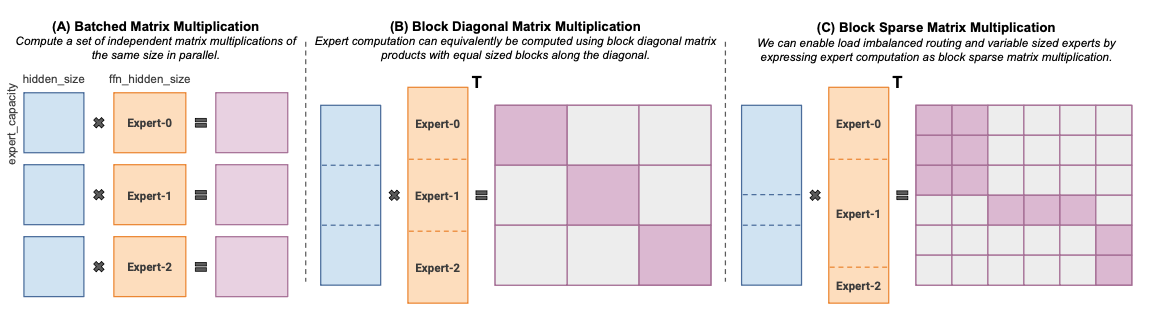
However, this efficiency comes at the cost of:
- Increased metadata management
- Padding overhead for block alignment
- Intermediate buffer allocation
These factors can limit practicality in memory-constrained environments.
DeepSeek-V2 Architecture
DeepSeek-V2 introduces a refined MoE design based on:
- Fine-grained experts: Smaller, more specialized expert networks
- Shared experts: Always-active experts that ensure representational capacity
- Routing bias mechanisms: Improved expert utilization without heavy auxiliary losses
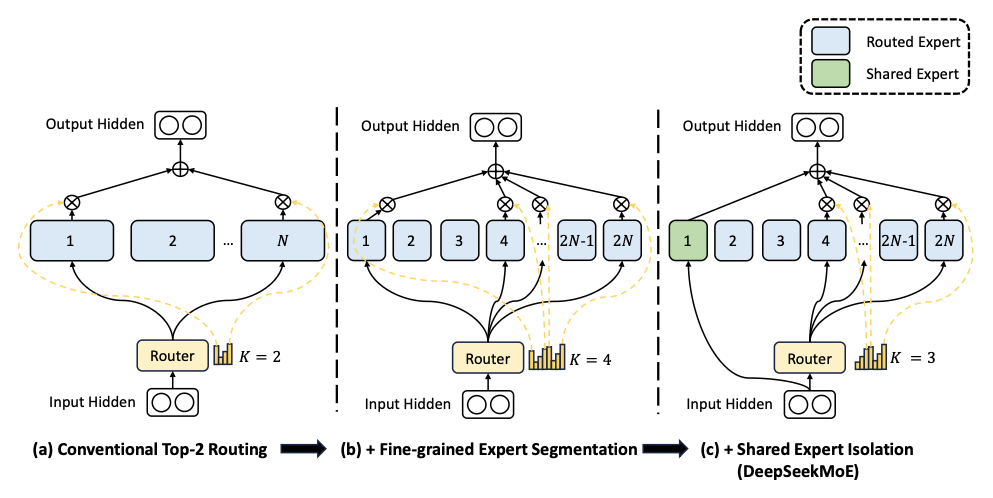
These architectural choices reduce reliance on explicit auxiliary losses and improve convergence behavior, motivating their evaluation beyond large-scale distributed settings.
Experimental Design
Model Variants
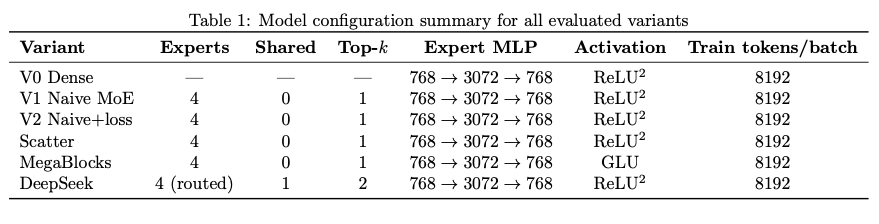
We evaluate six distinct configurations, progressively introducing MoE components and optimizations:
V0: Dense Baseline (Modded NanoGPT)
Our starting point uses the Modded NanoGPT configuration with:
- Compiled execution via
torch.compile - Flash Attention (scaled dot product attention)
- bfloat16 mixed precision
- Standard feed-forward layers (768 → 3072 → 768)
This serves as the reference for throughput and memory on single-GPU hardware.
V1: Naive MoE (Masked Compute, Top-1)
The dense MLP is replaced by a Mixture-of-Experts MLP with 4 experts and top-1 routing. To keep execution compile-friendly, the implementation evaluates all experts on the full token batch and applies a mask to accumulate only the selected expert output.
class MoEMLP(nn.Module):
def __init__(self, config):
super().__init__()
self.num_experts = 4
self.experts = nn.ModuleList([
MLP(config) for _ in range(self.num_experts)
])
self.router = nn.Linear(config.n_embd, self.num_experts, bias=False)
def forward(self, x):
# Compute routing weights
routing_weights = F.softmax(self.router(x), dim=-1)
# Evaluate ALL experts (inefficient but compile-friendly)
expert_outputs = torch.stack([expert(x) for expert in self.experts])
# Apply routing mask
selected_experts = routing_weights.argmax(dim=-1)
mask = F.one_hot(selected_experts, self.num_experts)
return torch.sum(expert_outputs * mask.unsqueeze(-1), dim=0)
This eliminates data-dependent control flow but increases activation and intermediate compute substantially.
V2: Naive MoE + Routing Losses (Top-1)
The MoE structure remains 4 experts with top-1 routing, but training adds explicit router regularization:
- Switch-style load balancing: Encourages uniform expert usage
- Router z-loss: Prevents routing logits from blowing up
- Importance-variance loss: Encourages diversity in expert selection
# Load balancing loss
expert_counts = F.one_hot(selected_experts, self.num_experts).float()
load_balance_loss = expert_counts.var(dim=0).mean()
# Router z-loss (logit magnitude regularization)
router_logits = self.router(x)
z_loss = torch.logsumexp(router_logits, dim=-1).pow(2).mean()
# Combined auxiliary loss
aux_loss = load_balance_loss + 0.01 * z_loss
V3: ScatterMoE (Kernelized Routing)
This variant replaces naive expert execution with ScatterMoE-style token dispatch and expert computation. The core design avoids redundant expert evaluation by:
- Gathering tokens per expert
- Executing expert MLPs on compacted batches
- Scattering outputs back to original positions
V4: MegaBlocks (Grouped Block-Sparse MoE)
We integrate MegaBlocks MoE with:
- 4 experts and top-1 routing
- Grouped execution (
mlp_impl="grouped") - GLU experts (
mlp_type="glu") - Layout transposes between batch-first and sequence-first representations
V5: DeepSeek (Shared + Routed Experts)
We implement a DeepSeek-style MoE layer with:
- 1 shared expert (always active)
- 4 routed experts (selected via top-2 routing)
- Two-pass computation: shared experts first, then routed experts
class DeepSeekMoE(nn.Module):
def __init__(self, config):
super().__init__()
self.shared_expert = MLP(config)
self.routed_experts = nn.ModuleList([
MLP(config) for _ in range(4)
])
self.router = nn.Linear(config.n_embd, 4, bias=False)
def forward(self, x):
# Shared expert (always active)
shared_out = self.shared_expert(x)
# Routed experts (top-2 selection)
routing_weights = F.softmax(self.router(x), dim=-1)
top_k_weights, top_k_indices = routing_weights.topk(2, dim=-1)
# Compute routed expert outputs
routed_out = torch.zeros_like(x)
for i in range(4):
mask = (top_k_indices == i).any(dim=-1)
if mask.any():
expert_out = self.routed_experts[i](x[mask])
routed_out[mask] += expert_out * top_k_weights[mask, :]
return shared_out + routed_out
Training Configuration
Dataset: FineWeb-10B binary shards
- Cleaned and deduplicated English web data from CommonCrawl
- 0.73B tokens used for training
- Sequence length: 2048 tokens
Optimization:
- Optimizer: AdamW with fused kernels
- Learning rate: 3e-4 with cosine decay
- Batch size: 8,192 tokens (4 sequences × 2048)
- Training steps: 12,000
- Mixed precision: bfloat16
Hardware:
- NVIDIA A100 GPU (40GB)
- Single-GPU training (no distributed parallelism)
Evaluation Metrics:
- Validation loss (measured every 500 steps)
- Average step time (milliseconds per training step)
- Peak allocated memory (PyTorch CUDA allocator)
- Reserved memory (includes allocator fragmentation and caching)
Results and Analysis
We evaluate all architectures for 12,000 training steps under identical optimization settings. All results are obtained from end-to-end training runs rather than microbenchmarks.
End-to-End Performance Comparison
| Variant | Val Loss | Step Avg (ms) | Peak Alloc (MiB) | Reserved (MiB) |
|---|---|---|---|---|
| V0 Dense | 4.0007 | 80.95 | 6,091 | 6,112 |
| V1 Naive MoE | 3.9821 | 149.08 | 11,339 | 13,792 |
| V2 Naive+Loss | 4.0427 | 151.19 | 11,340 | 13,794 |
| Scatter | 4.2197 | 125.39 | 9,320 | 9,518 |
| MegaBlocks | 4.5400 | 102.84 | 18,023 | 19,230 |
| DeepSeek | 3.9373 | 208.21 | 13,620 | 16,754 |
Key Observations:
-
Memory Pressure Dominates: Even the simplest MoE variants (V1, V2) require nearly 2× the peak allocated memory of the dense baseline, despite activating only a subset of experts per token
-
Kernel Strategy Impacts Latency: Naive MoE variants (V1, V2) exhibit the highest step times among non-DeepSeek models, reflecting redundant expert computation and routing overhead
-
MegaBlocks Memory Explosion: With nearly 19 GB of reserved memory, MegaBlocks exceeds practical limits of consumer GPUs, reflecting its design focus on large-scale distributed training
-
DeepSeek Convergence vs. Efficiency: DeepSeek achieves the lowest validation loss (3.94) but also the highest step time (208ms), representing a clear quality-efficiency trade-off
Throughput–Memory Trade-offs
Three distinct regimes emerge from our analysis:
1. Compute-Efficient but Memory-Heavy (MegaBlocks)
MegaBlocks achieves relatively low step time (102.84ms) through block-sparse operations, but incurs prohibitive memory overhead:
- Peak allocated: 18,023 MiB (3× dense baseline)
- Reserved memory: 19,230 MiB (includes allocator fragmentation)
The design optimizes for throughput in distributed settings with large batches, but the block construction metadata and padding overhead make it impractical for single-GPU training.
2. Balanced Systems Design (ScatterMoE)
ScatterMoE offers the best compromise between efficiency and memory:
- 16% faster than naive MoE (125.39ms vs 149.08ms)
- 18% lower memory than naive MoE (9,320 MiB vs 11,339 MiB)
By fusing routing operations and eliminating redundant expert computation, ScatterMoE demonstrates that careful kernel design can improve both dimensions simultaneously.
3. Optimization-Focused (DeepSeek)
DeepSeek prioritizes convergence quality over raw throughput:
- Lowest validation loss: 3.94 (vs 4.00 for dense baseline)
- Highest step time: 208.21ms (2.6× dense baseline)
- Moderate memory: 13,620 MiB (2.2× dense baseline)
The architectural complexity—shared experts, fine-grained routing, and multiple expert passes—increases per-step cost but delivers superior final model quality.
Convergence Behavior Analysis
While MoE architectures are primarily motivated by parameter efficiency, our results show that architecture design, not parameter count alone, determines convergence quality.
Naive MoE Variants (V1, V2)
Naive MoE achieves validation loss comparable to the dense baseline early in training (3.98 vs 4.00), but does not significantly outperform it despite activating more parameters per token. Adding explicit load-balancing losses (V2) actually degrades final validation loss to 4.04, suggesting that auxiliary routing objectives can interfere with optimization at small scale.
Kernel-Optimized Variants (Scatter, MegaBlocks)
Both ScatterMoE (4.22) and MegaBlocks (4.54) show degraded validation loss compared to the dense baseline, indicating that improving execution efficiency alone does not guarantee improved learning dynamics.
This phenomenon likely stems from:
- Expert underutilization due to load imbalance
- Routing instability from top-1 selection
- Representational fragmentation across experts
DeepSeek Architecture
In stark contrast, the DeepSeek-style architecture achieves the strongest convergence:
- Final validation loss: 3.94 (1.5% improvement over dense)
- Consistent improvement throughout training
- More stable loss curves with lower variance
This supports the hypothesis that fine-grained experts and shared capacity are more important for MoE effectiveness than routing efficiency alone. By ensuring that a portion of model capacity is always active (shared experts), the DeepSeek design avoids representational fragmentation observed in simpler MoE variants.
Systems-Level Insights
1. Memory, Not Compute, Is the Primary Bottleneck
Even modest expert counts (4 experts) quickly exhaust available VRAM:
- Activation storage for all experts (even masked ones in naive MoE)
- Routing intermediates (softmax outputs, expert assignments)
- Expert weight parameters (4× the feed-forward layer size)
This finding contradicts the common assumption that MoE’s benefit is primarily computational efficiency. On single GPUs, the memory cost of maintaining multiple experts dominates.
2. Kernel Specialization Is Necessary but Insufficient
ScatterMoE demonstrates that fused routing kernels can improve both throughput and memory efficiency. However, these gains do not translate to better convergence. This indicates that systems optimization and architectural design must be addressed jointly.
3. Architectural Choices Dominate Convergence
The DeepSeek architecture achieves superior convergence despite higher per-step cost, demonstrating that:
- Shared experts prevent representational collapse
- Fine-grained experts improve specialization
- Top-k routing (k>1) provides routing stability
These architectural properties matter more than raw throughput for final model quality.
4. Distributed Designs Don’t Translate to Single-GPU
MegaBlocks, designed for large-scale distributed training, performs poorly in our single-GPU setting:
- Block construction overhead
- Padding waste
- Metadata management
This highlights that MoE architectures optimized for datacenter deployments require fundamental redesign for consumer hardware.
Discussion and Practical Implications
When to Use MoE on Single GPUs
Our results suggest that MoE architectures are beneficial on single GPUs only when:
- Convergence quality is paramount: DeepSeek-style architectures can outperform dense baselines, but at significant computational cost
- Memory budget allows 2-3× overhead: All MoE variants require substantially more memory than dense models
- Training time is not critical: MoE variants are consistently slower per-step than dense baselines
For most single-GPU training scenarios, dense Transformers remain the most efficient choice.
Design Recommendations for Memory-Constrained MoE
Based on our findings, we propose the following design principles for single-GPU MoE training:
1. Prioritize Shared Capacity
Always include shared experts that process all tokens. This:
- Prevents representational fragmentation
- Provides stable gradient signal
- Improves convergence quality
2. Use Fused Routing Kernels
Implement ScatterMoE-style fused operations to:
- Eliminate redundant expert evaluation
- Reduce intermediate memory allocation
- Improve kernel launch efficiency
3. Limit Expert Count
With limited memory, fewer, larger experts outperform many small experts:
- Reduces routing overhead
- Improves expert utilization
- Decreases memory fragmentation
4. Employ Top-k Routing (k ≥ 2)
Top-1 routing creates instability and load imbalance. Top-2 or top-3 routing:
- Provides routing redundancy
- Smooths expert load distribution
- Improves optimization stability
Future Optimizations
Several promising directions could improve single-GPU MoE efficiency:
1. Gradient Checkpointing for Experts
Store only routing decisions during forward pass and recompute expert outputs during backward:
- Trades compute for memory
- Particularly effective with fast expert networks
- Can reduce peak memory by 30-40%
2. Mixed Granularity Experts
Combine coarse-grained shared experts with fine-grained routed experts:
- Shared experts handle general features (large, efficient)
- Routed experts handle specialized features (small, numerous)
3. Dynamic Expert Pruning
Progressively merge underutilized experts during training:
- Reduces effective expert count over time
- Maintains initial exploration capacity
- Improves final efficiency
4. Heterogeneous Expert Sizes
Not all experts need identical capacity:
- Frequently-used experts can be smaller (cache-friendly)
- Rarely-used experts can be larger (higher capacity)
Limitations and Future Work
Current Limitations
1. Limited Training Duration
Our 12,000-step experiments capture early training dynamics but may not fully reflect long-horizon behavior. Longer runs could:
- Further amplify convergence differences
- Reveal expert specialization patterns
- Expose optimization instabilities
2. Single Expert Type
All MoE variants replace only feed-forward sublayers. Unexplored directions include:
- Attention expert mixtures
- Depth-wise routing (skip connections to different layers)
- Hybrid dense-sparse architectures
3. Fixed Batch Size
We use a single batch size (8,192 tokens) across all variants. Different MoE implementations may have different optimal batch sizes:
- Larger batches may amortize MegaBlocks overhead
- Smaller batches may reduce naive MoE memory pressure
4. Hardware-Specific Results
All experiments use NVIDIA A100 GPUs. Results may differ on:
- Consumer GPUs (3080, 4090) with different memory hierarchies
- AMD GPUs with different kernel characteristics
- Future architectures with improved sparse compute
Future Research Directions
1. Adaptive Expert Allocation
Design systems that dynamically adjust expert count and size based on:
- Available memory
- Training progress
- Load imbalance metrics
2. Hybrid Parallelism Strategies
Explore combining:
- Expert parallelism (distribute experts across GPUs)
- Data parallelism (distribute batches)
- Pipeline parallelism (distribute layers)
Even on 2-4 consumer GPUs, these strategies could unlock larger MoE models.
3. Specialized Routing Mechanisms
Develop routing strategies tailored to single-GPU constraints:
- Locality-aware routing (prefer cache-resident experts)
- Batch-aware routing (balance load within mini-batch)
- Memory-aware routing (avoid peak allocation)
4. Compiler-Level Optimizations
Leverage emerging compiler technologies:
- Triton for custom routing kernels
-
torch.compilewith expert-aware fusion - JAX with expert parallelism primitives
Conclusion
This work presents a systems-oriented empirical study of Mixture-of-Experts training on a single, memory-constrained GPU, comparing dense Transformers with multiple MoE architectures and execution strategies.
Key Findings
1. Memory Dominates Over Compute
Across all MoE variants, memory pressure—not computational throughput—emerges as the primary bottleneck. Even modest expert counts (4 experts) require 2-3× the memory of dense baselines, fundamentally limiting MoE applicability on consumer hardware.
2. Kernel Optimization Improves Efficiency but Not Convergence
ScatterMoE demonstrates that fused routing kernels can simultaneously reduce step time (16% improvement) and memory usage (18% reduction) compared to naive implementations. However, these systems-level gains do not translate to better final model quality, highlighting the independence of execution efficiency and optimization dynamics.
3. Architectural Design Determines Convergence
The DeepSeek-inspired architecture achieves the best convergence (3.94 validation loss vs 4.00 dense baseline) through architectural innovations—shared experts, fine-grained specialization, and top-k routing—rather than kernel optimizations. This demonstrates that convergence quality stems from representational capacity, not execution speed.
4. Distributed Designs Don’t Transfer to Single-GPU
MegaBlocks, optimized for large-scale distributed training, achieves relatively low step time but incurs prohibitive memory overhead (19 GB reserved), rendering it impractical for single-GPU use. This underscores that MoE systems designed for datacenter environments require fundamental redesign for consumer hardware.
Practical Implications
For practitioners considering MoE on single GPUs:
- Dense models remain most efficient for typical single-GPU training scenarios
- MoE is viable only when convergence quality justifies 2-3× resource overhead
- Architectural choices (shared experts, routing strategy) matter more than kernel optimizations
- Successful MoE training requires co-design of architecture and systems implementation
Broader Impact
Our findings challenge the conventional narrative that MoE architectures uniformly improve efficiency. Instead, we demonstrate that MoE’s benefits are highly context-dependent:
- In distributed settings with abundant memory and parallelism, MoE can dramatically improve parameter efficiency
- On single GPUs with tight memory constraints, MoE often underperforms dense baselines
- Effective MoE requires careful alignment of architectural design, systems implementation, and hardware characteristics
This work highlights the importance of systems-aware architectural design in modern machine learning. As the field moves toward increasingly complex models, understanding the interplay between algorithm, implementation, and hardware becomes critical for practical deployment.
Resources
- Code Repository: GitHub - Modded NanoGPT MoE
- Technical Report: Full Paper (PDF)
- Presentation: Slides (PDF)
References:
-
Shazeer, N., Mirhoseini, A., Maziarz, K., Davis, A., Le, Q., Hinton, G., & Dean, J. (2017). Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. ICLR 2017.
-
Fedus, W., Zoph, B., & Shazeer, N. (2022). Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity. JMLR, 23(120), 1–39.
-
Gale, T., Zaharia, M., Young, C., & Shafahi, A. (2024). Scatter-MoE: Efficient sparse mixture-of-experts via token routing optimization. arXiv preprint arXiv:2403.08245.
-
Gale, T., Narayanan, D., Young, C., & Zaharia, M. (2023). MegaBlocks: Efficient sparse training with mixture-of-experts. Proceedings of MLSys, 5, 288–304.
-
DeepSeek-AI. (2024). DeepSeek-V2: A strong, economical, and efficient mixture-of-experts language model. arXiv preprint arXiv:2405.04434.
-
Dai, D., Deng, C., Zhao, C., et al. (2024). DeepSeekMoE: Towards ultimate expert specialization in mixture-of-experts language models. arXiv preprint arXiv:2401.06066.
-
Karpathy, A. (2024). Modded NanoGPT - NanoGPT speedrun baseline.